| The most important thing about energy is that it is conserved, which means that energy cannot be created or destroyed, it can only be converted into other kinds of energy. The total amount of energy remains constant. How many different kinds of energy are there? We know that mechanical energy consists of kinetic and potential energy, but energy can also appear in the form of heat, light, electric fields, magnetic fields, or even nuclear energy.
When we are talking about mechanical systems we are only concerned with kinetic and potential energy. Friction converts kinetic energy into heat, and so it represents a net loss of mechanical energy. Once energy is converted into heat it is for all practical purposes lost forever, because the heat will just drift off into the environment. This is what the brakes on a car do. In order to stop the car, the friction produced by the brake pads must generate a quantity of heat equal to the kinetic energy of the car, and as a result the brakes get very, very hot.
The law of conservation of energy can be stated in three (equivalent) ways:
- Energy cannot be created or destroyed, only changed into different kinds of energy.
- The total energy of an isolated system is constant. (An isolated system has no energy or mass entering or leaving it.)
- The Energy of an non-isolated system changes only by the amount added or removed. If the only energy involved is mechanical, this can be stated as W = DK + DPE, because the only way to change mechanical energy is to do work on the system. Doing work will either change the kinetic energy or the potential energy (or both) of the system.
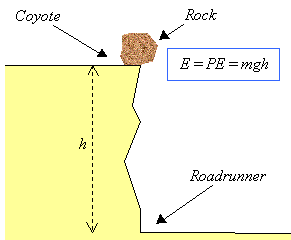
Example: Rock falling off cliff of height h (ignoring air friction)
Initially, the rock has a PE of mgh (the work it would require to raise it that high from ground level). At first this is also the total energy of the system, because potential energy is the only kind of energy the system has at that time.
As it falls it loses PE and gains KE, but always the total energy remains the same. Since it started with a total energy of mgh, this will always be the total energy. On the way down, its energy will be a mixture of PE and KE, but will still add up to that original value of mgh:
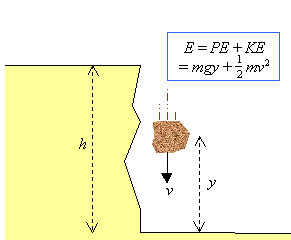
This means that at a given height y we can calculate the velocity. At a height y its PE is mgy and its KE is 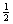 mv2, but their total is still the original amount of energy mgh, so mv2, but their total is still the original amount of energy mgh, so
mgh = mgy + 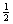 mv2, mv2,
from which it follows that
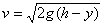 . .
Notice that we can find v at any point without knowing any details of the path!
At the very bottom, just before it hits, all the PE will be converted to KE,
so
mgh = 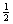 mv2 mv2
or 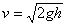
When the rock hits the bottom, all of the KE will be lost. Some will be spent breaking the rock and ground into pieces, some will go off as sound waves, and some willgo into doing work on the ground by compressing it. All this moving matter will experience friction, which converts KE into heat. Wherever all the energy goes, it must still add up to the original amount mgh.
Example: Block sliding down ramp with or without friction
Suppose a block is released form rest at the top of the ramp and allowed to slide down. How fast will it be going when it reaches the bottom? You could solve this problem by using the equations for constant acceleration, but it is much simpler to solve using conservation of energy.
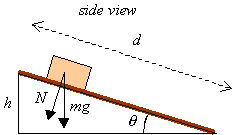
Without friction
The initial energy, when the block is at rest at the top of the ramp, is purely gravitational potential energy. If we measure the height h from the bottom of the ramp, the initial energy is
Ei = mgh
When the block reaches the bottom of the ramp. All of this potential energy will have been converted into kinetic energy, which is given by
Ef = 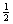 mv2 mv2
But because energy is conserved, and we are assuming that we are not losing any mechanical energy through friction, the initial and final energies must be equal. Thus
Ei = Ef
mgh = 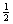 mv2 mv2
which can be solved to give the final velocity as
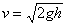
With friction
If we allow for friction while the block is sliding down the ramp, we have to take into account the amount of mechanical energy that will be lost due to friction. The work done against friction will be
Wf = Fkd,
where Fk is the force of kinetic friction,
Fk = Nmk,
And d is the distance traveled along the ramp. The normal force is
N = mg cos q
And the distance along the ramp, which is the hypotenuse of the triangle, is
d = h sin q
Putting all this together, we can get an expression for the work done against friction:
Wf = Fkd
= mk(mg cos
q)(h/sin q)
Wf = mgmkh
cot q
Now we can return to conservation of energy. The initial energy of the block is still
Ei = mgh,
and the final energy is still
Ef = 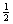 mv2, mv2,
But the initial and final energies are no longer equal because along the way we lost an amount Wf to kinetic friction. Thus
Ef = Ei – Wk
or
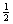 mv2 = mgh – mgmkh mv2 = mgh – mgmkh
cot q
which gives a final velocity of
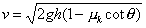
Example: Height to do loop–the–loop
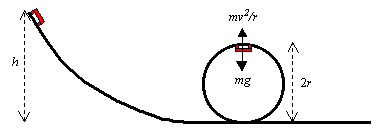
Suppose you were designing a roller coaster ride that featured a loop, as illustrated above. For simplicity we will assume that it is a frictionless roller coaster, even though that is not very realistic. You will need to figure out how high the car needs to start so that it has enough velocity to make it around the loop. The key observation is that the centrifugal force must be just enough to keep the car on the track when it is at the top of the loop. The centrifugal force is given by. From the car’s reference frame when it is at the top of the loop, this is an upward force which must counter the downward force of the car’s weight mg. Therefore we set mv2/r = mg, or
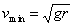
This is the minimun velocity that the car must have at the top of the loop. Now that we know the required velocity at this point, we can use conservation of energy. The initial energy, when the car starts from rest at the very top of the track, is all potential:
Ei
= mgh
The energy at the top of the loop is partly kinetic and partly potential, but now we know the velocity there, and we know that the height is twice the radius, so we can write an expression for the total energy:
Ef = mg(2r) + 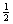 mv2 mv2
Ef = 2mgr +
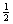 mgr mgr
Ef = 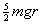
Now, because we are ignoring friction, we can set the initial energy equal to the final energy and solve for h:
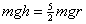 or or 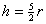
So, you need to start the track at a height that is 2.5 times the radius of the loop. Of course a real roller coaster will lose some energy to friction, and so you would have to start the track even higher |




