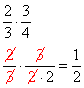Fractions
Fractions, also called rational numbers, are numbers of the form ![]() , where a and b are integers (but b cannot be zero).
, where a and b are integers (but b cannot be zero).
The bottom number is called the denominator. Think of it as the denomination: it tells you what size units you are talking about—fourths, fifths, or whatever. I have three of them: 3/4.
Improper Fractions
Ordinarily we think of fractions as being between zero and one, like 3/4 or 2/3. These are called proper fractions. In these fractions, the numerator is smaller than the denominator—but there is no reason why we can not have a numerator bigger than the denominator. Such fractions are called improper.
What does an improper fraction like 5/4 mean? Well, if we have 5 quarters of something then we have more than one whole of that something. In fact, we have one whole plus one more quarter (if you have 5 quarters in change, you have a dollar and a quarter).
Mixed Number Notation
One way of expressing the improper fraction 5/4 is as the mixed number ![]() , which is read as “one and one-fourth.” This notation ispotentially confusing and is not advised in algebra.
, which is read as “one and one-fourth.” This notation ispotentially confusing and is not advised in algebra.
One cause of confusion is that in algebra we use the convention that multiplication is implied when two quantitiesare written next to each other with no symbols in between. However, the mixed number notation implies addition, not multiplication. For example, 1 1\4 means 1 plusone-quarter, and 3 1/2 = 3 + 1/2.
It is possible to do arithmetic with mixed numbers by treating the whole number parts and the fractional parts separately, but it is generally more convenient in algebra to always write improper fractions. When you encounter a problem with mixed numbers, the first thing you should do is convert them to improper fractions.
Conversion
Mixed Number to Improper Fraction
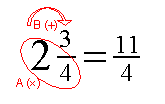
A. Multiply the integer part with the bottom of the fraction part.
B. Add the result to the top of the fraction.
The general formula is
![]()
Improper Fraction to Mixed Number
- Do the division to get the integer part
- Put the remainder over the old denominator to get the fractional part.
Multiplying, Reducing, and Dividing Fractions
Equivalent Fractions
Equivalent fractions are fractions that have the same value, for example
![]() etc.
etc.
Although all these fractions are written differently, they all represent the same quantity. You can measure a half-cup of sugar or two quarter-cups of sugar, or even four eighth-cups of sugar, and you will still have the same amount of sugar.
· Multiply by a form of One
A fraction can be converted into an equivalent fraction by multiplying it by a form of 1. The number 1 can be represented as a fraction any number divided by itself is equal to 1 (remember that the fraction notation means the same thing as division). In other words,
![]() etc.
etc.
Now if you multiply a number by 1 it does not change its value, so if we multiply a fraction by another fraction that is equal to 1, we will not be changing the value of the original fraction. For example,
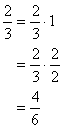
In this case, 2/3 represents exactly the same quantity as 4/6, because all we did was to multiply 2/3 by the number 1, represented as the fraction 2/2.
Multiplying the numerator and denominator by the same number to produce an equivalent fraction is called building up the fraction.
Reduced Form
Numerator and Denominator Have No Common Factors
Procedure:
1. Write out prime factorization of Numerator and Denominator
2. Cancel all common factors
This procedure is just the opposite of building up a fraction by multiplying it by a fraction equivalent to 1.
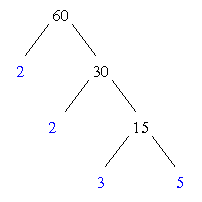
Prime FactorsA number is prime if it has no whole number factors other than 1 times itself, that is, the number cannot be written as a product of two whole numbers (except 1 times itself). Example: Example:
Any non-prime number can be decomposed into a product of prime numbers Example: Example: The Branching MethodThis method works well for larger numbers that might have many factors. All you need to do is think of any two numbers that multiply to give your original number, and write them below it. Continue this process for each number until each branch ends in a prime number. The factors of the original number are the prime numbers on the ends of all the branches.
Notes
|
Multiplying Fractions
Multiply Numerators and Denominators
Example:
![]()
And reduce result if needed
![]()
Canceling common factors first makes multiplication
easier
If you don’t reduce the factors before multiplying, the answer will have to be reduced.
Example:
Remember that canceling always leaves a “1” behind, because you are really dividing the numerator and the denominator by the same number.
Adding and Subtracting Fractions
· Add Numerators when Denominators Are the Same
![]()
· If the denominators are not the same, make them the same by building up the fractions so that they both have a common denominator.
· Any common denominator will work, but the answer will have to be reduced if it is not the Least Common Denominator.
· The product of all the denominators is always a common denominator (but not necessarily the Least Common Denominator).
Least Common Denominator (LCD)
By Inspection
The smallest number that is evenly divisible by all the denominators
In General
The LCD is the product of all the prime factors of all the denominators, each factor taken the greatest number of times that it appears in any single denominator.
- Example:
![]()
Factor the denominators:
![]()
![]()
Assemble LCD:
![]()
Note that the three only appears once, because it is only needed once to make either the 12 or the 15:
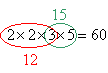
Now that you have found the LCD, multiply each fraction (top and bottom) by whatever is needed to build up the denominator to the LCD:
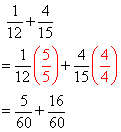
Then add the numerators and reduce if needed (using the LCD does not guarantee that you won’t have to reduce):
![]()