The Solutions of a System of Equations
A system of equations refers to a number of equations with an equal number of variables. We will only look at the case of two linear equations in two unknowns. The situation gets much more complex as the number of unknowns increases, and larger systems are commonly attacked with the aid of a computer.
A system of two linear equations in two unknowns might look like
![]()
This is the standard form for writing equations when they are part of a system of equations: the variables go in order on the left side and the constant term is on the right. The bracket on the left indicates that the two equations are intended to be solved simultaneously, but it is not always used.
When we talk about the solution of this system of equations, we mean the values of the variables that make both equations true at the same time. There may be many pairs of x and y that make the first equation true, and many pairs of x and y that make the second equation true, but we are looking for an x and y that would work in both equations. In the following pages we will look at algebraic methods for finding this solution, if it exists.
Because these are linear equations, their graphs will be straight lines. This can help us visualize the situation graphically. There are three possibilities:
1. Independent Equations
· Lines intersect
· One solution
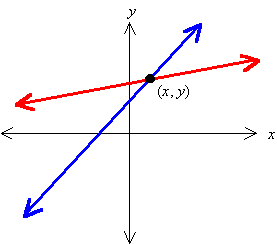
In this case the two equations describe lines that intersect at one particular point. Clearly this point is on both lines, and therefore its coordinates (x, y) will satisfy the equation of either line. Thus the pair (x, y) is the one and only solution to the system of equations.
2. Dependent Equations
· Equations describe the same line
· Infinite number of solutions
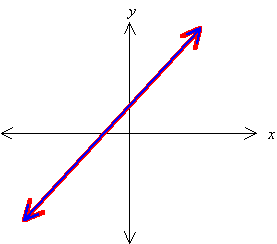
Sometimes two equations might look different but actually describe the same line. For example, in
![]()
The second equation is just two times the first equation, so they are actually equivalent and would both be equations of the same line. Because the two equations describe the same line, they have all their points in common; hence there are an infinite number of solutions to the system.
- Attempting to solve gives an identity
If you try to solve a dependent system by algebraic methods, you will eventually run into an equation that is an identity. An identity is an equation that is always true, independent of the value(s) of any variable(s). For example, you might get an equation that looks like x = x, or 3 = 3. This would tell you that the system is a dependent system, and you could stop right there because you will never find a unique solution.
3. Inconsistent Equations
- Lines do not intersect (Parallel Lines; have the same slope)
- No solutions
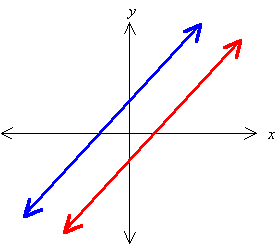
If two lines happen to have the same slope, but are not identically the same line, then they will never intersect. There is no pair (x, y) that could satisfy both equations, because there is no point (x, y) that is simultaneously on both lines. Thus these equations are said to be inconsistent, and there is no solution. The fact that they both have the same slope may not be obvious from the equations, because they are not written in one of the standard forms for straight lines. The slope is not readily evident in the form we use for writing systems of equations. (If you think about it you will see that the slope is the negative of the coefficient of x divided by the coefficient of y).
- Attempting to solve gives a false statement
By attempting to solve such a system of equations algebraically, you are operating on a false assumption—namely that a solution exists. This will eventually lead you to a contradiction: a statement that is obviously false, regardless of the value(s) of the variable(s). At some point in your work you would get an obviously false equation like 3 = 4. This would tell you that the system of equations is inconsistent, and there is no solution.
|
