Graphing Functions
Consider an equation such as
y = 2x – 1
We say that y is a function of x because if you choose any value for x, this formula will give you a unique value of y. For example, if we choose x = 3 then the formula gives us
y = 2(3) – 1
or
y = 5
Thus we can say that the value y = 5 is generated by the choice of x = 3. Had we chosen a different value for x, we would have gotten a different value for y. In fact, we can choose a whole bunch of different values for x and get a y value for each one. This is best shown in a table:
|
x (Input) |
x→FORMULA→ y |
y (Output) |
|
–2 |
2(–2) – 1 = –5 |
–5 |
|
–1 |
2(–1) – 1 = –3 |
–3 |
|
0 |
2(0) – 1 = –1 |
–1 |
|
1 |
2(1) – 1 = 1 |
1 |
|
2 |
2(2) – 1 = 3 |
3 |
|
3 |
2(3) – 1 = 5 |
5 |
This relationship between x and its corresponding y values produces a collection of pairs of points (x, y), namely
(–2, –5)
(–1, –3)
(0, –1)
(1, 1)
(2, 3)
(3, 5)
Since each of these pairs of numbers can be the coordinates of a point on the plane, it is natural to ask what this collection of ordered pairs would look like if we graphed them. The result is something like this:
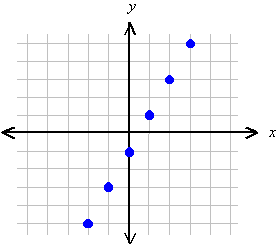
The points seem to fall in a straight line. Now, our choices for x were quite arbitrary. We could just as well have picked other values, including non-integer values. Suppose we picked many more values for x, like 2.7, 3.14, etc. and added them to our graph. Eventually the points would be so crowded together that they would form a solid line:
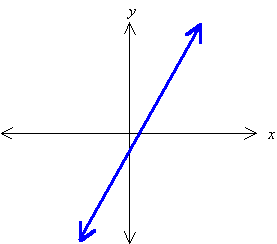
The arrows on the ends of the line indicate that it goes on forever, because there is no limit to what numbers we could choose for x. We say that this line is the graph of the function y = 2x – 1.
If you pick any point on this line and read off its x and y coordinates, they will satisfy the equation y = 2x – 1. For example, the point (1.5, 2) is on the line:
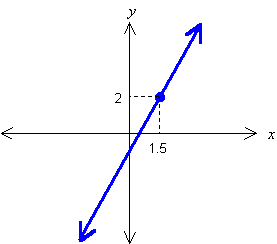
and the coordinates x = 1.5, y = 2 satisfy the equation y = 2x – 1:
2 = 2(1.5) – 1
· Note: This graph turned out to be a straight line only
because of the particular function that we used as an example. There are many
other functions whose graphs turn out to be various curves.
