Circular Motion

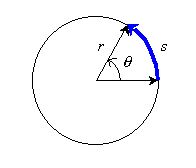
Uniform Circular Motion

By uniform circular motion, we mean motion in a circle at constant speed. Circular motion is very common, for example, many of our machines involve rotating parts. If an object is traveling in a circle we could describe its motion with the usual variables for position, velocity, and acceleration, but it would be complicated because
the object’s direction is constantly changing. It is more convenient to define new variables to describe circular motion in angular units.

Angular Measure

To locate the position of the object on the circle, we only need to specify an angle. Angles are often represented by the Greek letter theta (q). This variable plays the same role in rotational motion formulas that the letter x plays in linear motion formulas. Although we often measure angles in degrees, the standard SI unit for angle is the radian. An angle in radians is defined to be the ratio of arc length to radius along a circle:

There are 2p radians in a full circle, so the conversion between degrees and radians is

360° = 2p radians

or you can eliminate a 2 and say

180° = p radians

Angular Velocity

Recall that average linear velocity v was defined as the change in position per change in time, or

To define angular velocity, we follow the same definition but we use the change in angle per change in time. Angular velocity is represented by the lower-case Greek letter omega, (w), and is defined by

This definition gives us the formula

q = q₀ + w t,

which is the angular analog to the equation

x = x₀ + v t,

and like that equation is only valid for constant (or average) velocity.

The relation between angular and linear velocity

An object traveling in a circle will still have a linear velocity v. The direction of this velocity is constantly changing, but at any instant it points in a direction tangent to the circle (and perpendicular to the radius).

The magnitude of this velocity is related to the radius r and the angular velocity w by

v = w r

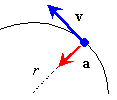
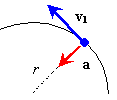
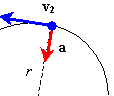
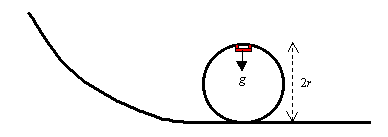
This can be shown by considering a time interval t. During this time the objectwill travel an angle q = w t, and a distance equal to the arc length s = rq. Velocity is distance per time, so

Centripetal Acceleration

If an object is traveling in a circle then it is accelerating, even if its speed is constant. This is because velocity is a vector, and so a change in direction is a change in velocity, and acceleration is the change in velocity per change in time. A turning type of acceleration is a sideways acceleration. Along the circle, this means that the acceleration is along the radius, pointing toward the center of the circle.

This particular acceleration that causes an object to travel in a circle, is called a centripetal acceleration, which means a center-seeking acceleration. Like any acceleration it is defined by

We have to consider the vector nature of velocity to determine Dv, because the only change is in its direction. Although a proper derivation requires calculus, the following diagrams should at least suggest that the change in velocity points in the inward radial direction:

It can be shown that the magnitude of the centripetal acceleration is

Example

How fast do you need to be going to maintain contact with a track doing a vertical loop of radius r?

When you are at the top of the loop you will have a downward acceleration produced entirely by gravity, and we know that the acceleration due to gravity is g. To keep you on the circle, this acceleration must serve as the centripetal acceleration, so

ac = g ,

or

or

Angular Acceleration

So far we have only been discussing uniform, or constant-speed circular motion. It is also possible for the angular velocity to be changing, and we call this an angular acceleration. Do not confuse this with the centripetal acceleration. Centripetal acceleration is always present in circular motion because it keeps the object turning in a circle, and it always points along the radius toward the center of the circle. If the object is speeding up or slowing down then it also has another acceleration, this time in a direction tangent to the circle. This acceleration can be expressed in angular
variables. We use the lower-case Greek letter alpha (a) for angular acceleration, and define it as the change in angular velocity per time interval:

We can also express it as a linear acceleration a, but you must keep in mind that this is not the total acceleration because there is also a centripetal acceleration. However, if we are only interested in the tangential component of the acceleration, we can find it from a by using the formula

Note that for uniform circular motion, both a and tangential will be zero, but there will always be a centripetal acceleration equal to v²/r.

Constant Acceleration Formulas

Because the angular variables q, w, and a are defined the same way as their linear
counterparts x, v¸ and a, all the formulas that we derived for constant acceleration can also be used for angular variables. For example, the equation

becomes