Quadratic Equations
Definition
ax2 + bx + c = 0
a, b, c are constants (generally integers)
Roots
Synonyms: Solutions or Zeros
- Can have 0, 1, or 2 real roots
Consider the graph of quadratic equations. The quadratic equation looks like ax2 + bx + c = 0, but if we take the quadratic expression on the left and set it equal to y, we will have a function:
y = ax2 + bx + c
When we graph y vs. x, we find that we get a curve called a parabola. The specific values of a, b, and c control where the curve is relative to the origin (left, right, up, or down), and how rapidly it spreads out. Also, if a is negative then the parabola will be upside-down. What does this have to do with finding the solutions to our original quadratic equation? Well, whenever y = 0 then the equation y = ax2 + bx + c is the same as our original equation.
Graphically, y is zero whenever the curve crosses the x-axis. Thus, the solutions to the original quadratic equation (ax2 + bx + c = 0) are the values of x where the function (y = ax2 + bx + c)crosses the x-axis. From the figures below, you can see that it can cross the x-axis once, twice, or not at all.
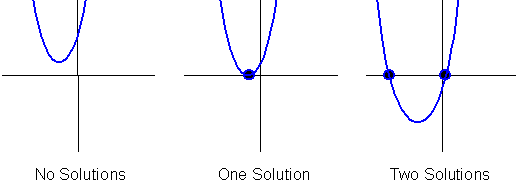
|
Your graphing calculator most likely has a function that will automatically find these intercepts and give you the x-values with great precision. Of course, no matter how many decimal places you have it is still just an approximation of the exact solution. In real life, though, a close approximation is often good enough. |
