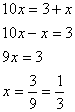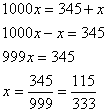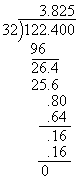Decimals

Decimals are Really Just Fractions

Decimal notation is just a shorthand way of expressing certain fractions, namely those fractions with denominators that are powers of 10. For example, consider the number

2.345

Because of the place-values of the decimal digits, this really means

Converting Decimals to Fractions

Because all the denominators are powers of 10, it is very easy to add these fractions by finding a common denominator. In this example, the common denominator is 1000, and we get

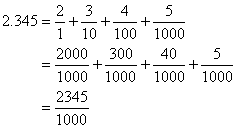
This suggests a general rule for converting a decimal number to its fraction form:

Put all the digits over the denominator that corresponds to the last decimal place value.

In the number 2.345, the last decimal place value is the thousandths place, so we put the digits 2345 over the denominator 1000.

Of course we would usually want to reduce the resulting fraction to its simplest form. In this case

The only time this method does not work is for repeating fractions. We know that 1/3 = 0.3333333... but how could we go from 0.3333333... back to 1/3? There is no ‘last decimal place’ because the decimals repeat forever. Fortunately, there is a simple trick for this:

· Put the repeating digit over a denominator of 9.

So we see that in the case of 0.3333333...., the repeating digit is 3, and we make the fraction 3/9, which reduces to 1/3.

If there is a group of more than one digit that repeats,

Put the repeating group of digits over as many 9’s as there are digits.

For example, in the fraction

we see that the group of digits ‘15’ repeats, so we put ‘15’ over a denominator of ‘99’ to get

o One warning: This only works for the repeating fraction part of a number. If you have a number like 2.33333..., you should just work with the decimal part and rejoin it with the whole part after you have converted it to a fraction.

o Irrational numbers like p or have non-repeating decimals, and so they cannot be written as fractions. You can, however, round them off at some point and produce an approximate fraction for them.

Why This Trick Works

If you have learned enough algebra to follow these steps, it is not difficult to see why this works. Let’s start with the simple example 0.3333333... Since we already know that the answer is 1/3, we can concentrate on the procedure, not the answer.

Let

x = 0.3333333...

Multiply both sides by 10 to get

10x = 3.33333...

Notice that the decimal part (.33333…) is still the same. In fact, it is the very thing that we called x in the first place, so we can say that

10x= 3 + x

Now solve for x:

This method will also work for repeating fractions that contain a group of repeating digits, but you have to multiply by a higher power of 10 in order to make the decimal portion stay the same as it was before. For example, suppose we had 0.345345345....

Let

x = 0.345345345....

Multiply both sides by 1000 to get

1000x = 345.345345345....

Notice that the decimal part is still the same. In fact, it is still the thing that we called x in the first place, so we can say that

1000x = 345 + x

Now solve for x:

Converting Fractions to Decimals

We know the decimal equivalents for some common fractions without having to think about it: 1/2 = 0.5, 3/4 = 0.75, etc. But how do we arrive at these numbers? Remember that the fraction bar means the same thing as division.

To convert a fraction to a decimal, do the division.

For example,

You can do the division with a calculator or by hand with long division.

Rounding

Look only one digit to the right
‘5’s or higher round up (there is some dispute about this rule, but it is good enough for most purposes)

Rounding 5’s

Why round fives up? The number 3.5 is exactly halfway between 3.0 and 4.0, so it makes just as much sense to round it down as it does to round it up.

Most of the time there is no harm in using the ‘always round fives up’ rule. This is the rule that the United States Internal Revenue Service advises you to use on your taxes, and who is going to argue with them?

Sometimes, though, it can cause problems. Suppose you are adding a very large number of values that have all been rounded by this rule. The sum that you get will be a little bit bigger than it ought to be. This can be a very serious problem in computer programs. When thousands or even millions of additions are being performed, the accumulated roundoff error can be quite large.

One way of dealing with this problem is the even-odd rule. This rule says that:

If the five is the last significant digit and the round-off digit (the one to the left of the 5) is odd, round up.
If the five is the last significant digit and the round-off digit is even, don’t round up.

Actually, you could reverse even and odd in this rule. All that matters is that about half the time you will be rounding up on a 5, and half the time down.

The reason it matters that the five is the last significant digit is because if there are any other non-zero digits past the five then you must round up, because the part that you are chopping off is more than 50% of the roundoff place-value. For example, suppose you want to round 3.351 to the nearest tenth. The decimal part represents the fraction 351/1000, which is 1/1000 closer to 400/1000 than it is to 300/100. Therefore you would always round this up to 3.4.

Example: Round 11.3826 to the nearest hundredth.

Solution: The hundredths place is where the ‘8’ is. We look one digit to the right and see a ‘2’, so we do not round up, leaving us with 11.38.

Example: Round 11.3826 to the nearest thousandth.

Solution: The thousandths place is where the ‘2’ is. We look one place to the right and see a ‘6’, so we round the ‘2’ up, getting 11.383.

Trouble with ‘9’s.

If the digit you are rounding up is a ‘9’, then rounding it up will make it a ‘10’, which is too big for one place. What happens is that the extra ‘1’ gets added to the place to the left.

Example: Round 3.49721 to the nearest hundredth.

Solution: The hundredth place has a ‘9’ in it. One step to the right is a ‘7’, so we have to round up. This makes the ‘9’ into a ‘10’, but we really can’t write the new number as 3.4(10). Instead, the extra ‘1’ moves one place to the left and is added to the ‘4’, giving us 3.50.

It can happen that the place to the left contains another ‘9’, in which case the extra ‘1’ will cause it to become a ‘10’, which pushes the ‘1’ still further on to the next place to the left.

Example: Round 75.69996217 to the nearest ten-thousandth

Solution: The ten-thousandths place is the last ‘9’ in the number, and the place to its right is a ‘6’, which means we round up. This makes the ‘9’ into a ‘10’, like this:

75.699(10)

But of course we cannot put a ‘10’ in that place, so the ‘1’ moves to the left and gets added to the ‘9’ there, making it into a ‘10’:

75.69(10)0

This leaves us with the same problem, a ‘10’ in one decimal place, so the extra ‘1’ moves one more step to the left, turning that ‘9’ into a ‘10’:

75.6(10)00

Well, we still have the same problem, so we move the ‘1’ yet another step to the left, where it adds on to the ‘6’, finally leaving us with an acceptable answer:

75.7000

In general,

· The extra ‘1’ migrates to the left until it finds a resting-place.

This means that the ‘1’ moves to the left until it can be added to a digit less than ‘9’, or until it falls off the end as a new digit out in front.

Example: Round 999.96 to the nearest tenth.

The digit to the right of the tenths place is a ‘6’, so we have to round up. But when we round up the ‘9’ it becomes a ‘10’, forcing the one to be added to the left. Unfortunately, we find another ‘9’ there and the process is repeated for each of the ‘9’s until we reach the leading ‘9’, which becomes a ‘10’ resulting in 1000.0

Arithmetic with Decimals

Although calculators have made it much easier to do arithmetic with decimal numbers, it is nice to know that you can still do it without a calculator.

Addition and Subtraction

To add or subtract decimal numbers, you use the familiar column method that you learned back in grade school. To use this method, the place values of the two numbers must be lined up. This means that the decimal points must be lined up, and you can fill in with zeros if one number has more decimal places than the other.

Example:

5.46 + 11.2

Becomes:

Multiplication

To multiply two decimal numbers, you can use the column method just as you would with whole numbers. You ignore the decimal points as you carry out the multiplication, and then you put the decimal point in the result at the correct place. The product will have the number of decimal places as the total number of decimal places in the factors. In the following example, the first factor has 2 decimal places and the second factor has 1 decimal place, so the product must have 3 decimal places:

Division

You can divide decimal numbers using the familiar (?) technique of long division. This can be awkward, though, because it is hard to guess at products of decimals (long division, you may recall, is basically a guess-and-check technique). It can be made easier by multiplying both the dividend and divisor by ‘10’s to make the divisor a whole number. This will not change the result of the division, because division is the same thing as fractions, and multiplying both the numerator and denominator of a fraction by the same number will not change the value of the fraction. For example, consider