Rectangular Coordinates
The rectangular coordinate system is also known as the Cartesian coordinate system after Rene Descartes, who popularized its use in analytic geometry. The rectangular coordinate system is based on a grid, and every point on the plane can be identified by unique x and y coordinates, just as any point on the Earth can be identified by giving its latitude and longitude.
Axes
Locations on the grid are measured relative to a fixed point, called the origin, and are measured according to the distance along a pair of axes. The x and y axes are just like the number line, with positive distances to the right and negative to the left in the case of the x axis, and positive distances measured upwards and negative down for the y axis. Any displacement away from the origin can be constructed by moving a specified distance in the x direction and then another distance in the y direction. Think of it as if you were giving directions to someone by saying something like “go three blocks East and then 2 blocks North.”
Coordinates, Graphing Points
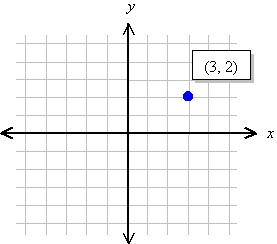
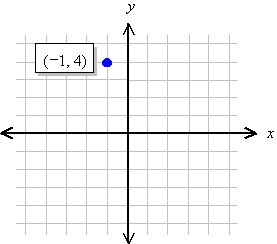
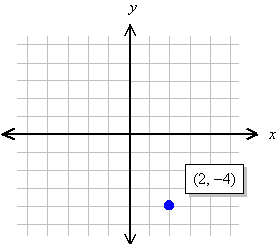
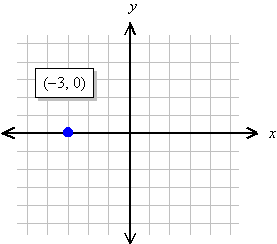
We specify the location of a point by first giving its x coordinate (the left or right displacement from the origin), and then the y coordinate (the up or down displacement from the origin). Thus, every point on the plane can be identified by a pair of numbers (x, y), called its coordinates.
Examples:
 |
 |
 |
 |
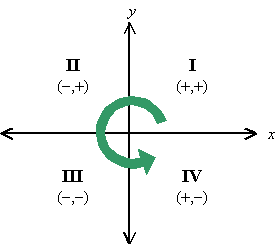
Quadrants
Sometimes we just want to know what general part of the graph we are talking about. The axes naturally divide the plane up into quarters. We call these quadrants, and number them from one to four. Notice that the numbering begins in the upper right quadrant and continues around in the counter-clockwise direction. Notice also that each quadrant can be identified by the unique combination of positive and negative signs for the coordinates of a point in that quadrant.