| Definition: rate of change of velocity
Standard Units: meters per second per second (m/s2) Average AccelerationAcceleration is the change in velocity per time interval. Note that this formula leads to units of m/s2 because velocity is m/s and time is s. This formula can be rearranged, with some changes to the symbols, to give
Here v means the velocity right now, v0 means the initialvelocity, and t is the elapsed time. It is important to remember that this formula is only valid if the acceleration is constant, because it comes from the formula for average acceleration. “Deceleration” is just negative acceleration. If the velocity is decreasing then Dv (Dv means ‘the change in velocity’) will be negative. Thus, the brake pedal in your car is also an accelerator, but with a minus sign on it. Because velocity is a vector, acceleration is also a vector. If a velocity vector changes direction, then it is a different vector and so Dv is not zero—even if the speed remains the same. What this means is:
So even turning counts as acceleration. Thus the steering wheel in your car is also a kind of accelerator. If you think about it, this makes sense because you feel acceleration whenever you speed up, slow down, or turn. Think about trying to hold a full drink without spilling it when your car is doing any of these things. But if your car is going in a straight line at constant speed, then there is no acceleration and you are not in danger of spilling your drink. This point is worth repeating:
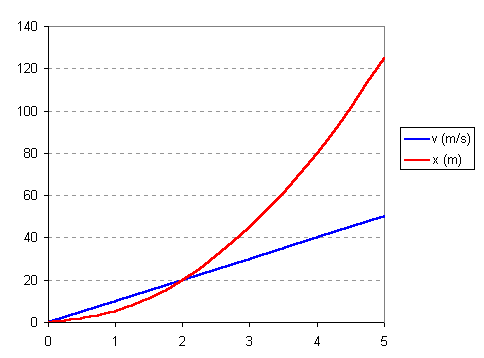
Units for accelerationThe standard SI units for acceleration is a meter per second per second, meaning an acceleration that increases the velocity by one meter/second every second. This is usually express as one m/s2. Another unit commonly used for acceleration is g’s. A g is the acceleration due to gravity on the Earth’s surface. It is about 9.8 m/s2, or 32 ft/s2. This means that for every second of free-fall, your speed increases by 32 feet per second. So after one second your speed is 32 ft/s, after two seconds it is 64 ft/s, after three seconds it is 96 ft/s, and so on (this is ignoring air friction, which becomes significant at high speeds and will eventually stop the acceleration of a falling body). An F-16 fighter can take a 9-g turn, but the pilots can’t without blacking out. About the most that humans can tolerate and still function (sort of) is about 6 g’s. Human tolerance depends on both the acceleration and the length of time the acceleration is endured. People can tolerate 45g for 0.1 seconds or 10 g for 1 second. In a car crash with seat belts, the acceleration is about 100g for 0.03 seconds, which is survivable, but an acceleration of 100g for 0.10 seconds would be fatal (the aorta ruptures from the pressure buildup). Graphical InterpretationsExample Data: Constant a = 10 m/s Suppose a mass is starting from rest (v = 0), and accelerates at a constant 10 m/s2. If we take a snapshot at one-second intervals, we can calculate its velocity and the distance traveled as follows:
We have to use the average velocity to calculate the new distance, because the velocity is not a constant (it is accelerating).
Acceleration ExampleZero to 60 mph in 3 seconds, expressed in “g“s |