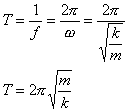Many systems oscillate: springs, pendulums, radio waves,etc. The common feature of all oscillating systems is the presence of a restoring force, which means that if the system is moved away from its equilibrium position, a force will arise that pushes it back towards the equilibrium position. We will take as our “prototype” the mass on the end of an
ideal spring.

Descriptive Variables

x = current displacement from resting position (in
meters)

A = Amplitude, the maximum value of the displacement

T = Period, the time for one complete cycle (in seconds)

f = 1/T = Frequency, the number of cycles per second (in Hertz)

w =2pf = Angular frequency, in radians/second

Simple Harmonic Oscillation

An oscillation is called simple harmonic oscillation (SHO) if the restoring force obeys Hooke’s Law. In this case the oscillation will be sinusoidal.

Hooke’s Law: F = –kx

Where k is a constant that is a property of the particular spring.

A force equation like this can be solved to give an equation of motion, but this is a calculus task and so we will jump directly to the solution, which gives the displacement x as a function of the time t.

Solution: x = A cos(wt – f)

Where A is the maximum displacement, w is the angular frequency, and f is the phase at t = 0. Normally we would start it with f = 0, so the phase is not something we need to worry about right now.

The angular frequency w is defined by

and the period T can be found from this:

Energy in an oscillating Spring

As a spring is stretched a distance x from equilibrium, work is done as a force is exerted over a distance. Complicating
things in this case is the fact that the force is not constant, so we cannot simply multiply the final force times the total distance. It turns out that we can use the average force (it is not always true that one can simply substitute the average for a changing quantity–the “real” solution is a calculus problem).

Since the force starts out at zero and ends up being kx, the average force is one-half kx. Multiplying this be the distance x gives us the work done in stretching the spring, which is also equal to the potential energy stored in the stretched spring:

As the mass passes through the equilibrium position, the potential energy will have all been converted to kinetic energy. Then the mass will start slowing down as this KE is turned back into PE. When it reaches its furthest extent, its velocity is momentarily zero and its energy is all potential. At any moment, of course, the total energy is constant.