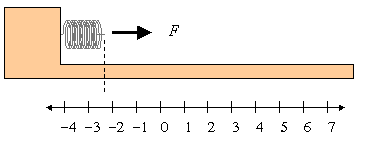| A substance is elastic if it behaves like a spring: If you stretch it or compress it, it will try to return to its original shape. We say that it produces a restoring force, because the force always points back to its resting position. You may be slightly confused by the directions of the forces in the diagrams below. Remember that we are talking about the force that the spring exerts, not the external force that must be applied to stretch or compress it in the first place. To stretch the spring, you may have to pull it to the right. The spring will respond by exerting a force in the opposite direction, to the left (remember Newton’s third law?).
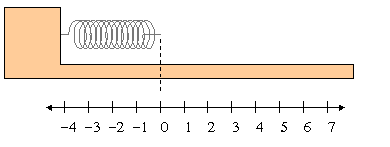
1. Relaxed Spring: Zero Force
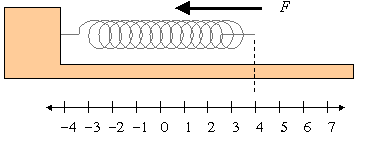
2. Stretched Spring: Restoring Force (displacement in the positive direction, force in the negative direction)
3. Compressed Spring: Restoring Force (displacement in the negative direction, force in the positive direction) Another property of springs is that the force increases as the displacement increases. We can express this relation is a formula, known as Hooke’s law:
It should be obvious that no real spring can obey Hook’s law for all values of x. You can only compress a spring up to the point where its coils touch, and if you stretch it too far it won’t spring back anymore, and it may even break. It must be kept in mind, then, that Hook’s law can only be used when the size of the displacement is small enough. With this in mind, Hook’s law is extremely useful and can be used to describe a wide variety of elastic systems, but it doesn’t apply to everything. |