Addition and Subtraction of Real Numbers

All the basic operations of arithmetic can be defined in terms of addition, so we will take it as understood that you have a concept of what addition means, at least when we are talking about positive numbers.

Addition on the Number Line

A positive number represents a distance to the right on the number line, starting from zero (zero is also called the origin since it is the starting point). When we add another positive number, we visualize it as taking another step to the right by that amount. For example, we all know that 2 + 3 = 5. On the number line we would imagine that we start at zero, take two steps to the right, and then take three more steps to the right, which causes us to land on positive 5.

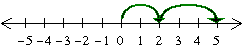
Addition of Negative Numbers

What does it mean to add negative numbers? We view a negative number as a displacement to the left on the number line, so we follow the same procedure as before but when we add a negative number we take that many steps to the left instead of the right.

Examples: 

2 + (–3) = –1

First we move two steps to the right, and then three steps to the left:

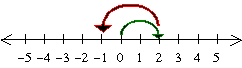
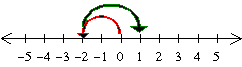
(–2) + 3 = 1

We move two steps to the left, and then three steps to the right:

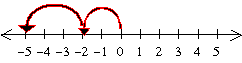
 (–2) + (–3) = –5

Two steps to the left, and then three more steps to the left:

 

From these examples, we can make the following observations:

1.      If we add two positive numbers together, the result will be positive

2.      If we add two negative numbers together, the result will be negative

3.      If we add a positive and a negative number together, the result could be positive or negative, depending on which number represents the biggest step.

 Subtraction

There are two ways to define subtraction: by a related addition statement, or as adding the opposite.

Subtraction as Related Addition

a – b = c if and only if a = b + c

Subtraction as Adding the Opposite

For every real number b there exists its opposite –b, and we can define subtraction as adding the opposite:

a – b = a + (-b)

·        In algebra it usually best to always think of subtraction as adding the opposite

Distinction Between Subtraction and Negation

The symbol “–” means two different things in math. If it is between two numbers it means subtraction, but if it is in front of one number it means the opposite (or negative) of that number.

Subtraction is binary (acts on two numbers), but negation is unary (acts on only one number).

          Calculators have two different keys to perform these functions. The key with a plain minus sign is only for subtraction:

 

Negation is performed by a key that looks like one of these:

Remember that subtraction can always be thought of as adding the opposite. In fact, we could get along just fine without ever using subtraction.

Subtraction on the Number Line

Addition of a positive number moves to the right, and adding a negative moves to the left.

Subtraction is just the opposite: Subtraction of a positive number moves to the left, and subtracting a negative moves to the right.

·     Notice that subtracting a negative is the same thing as adding a positive.