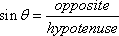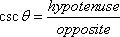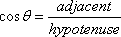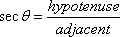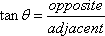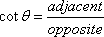The Trigonometric Functions in Right Triangles

The Trigonometric Functions in Right Triangles

The trigonometric functions are actually nothing more than ratios of the sides of right triangles (at least for now–later we will see a more general definition of the trigonometric functions). To see how this works, consider a right triangle:

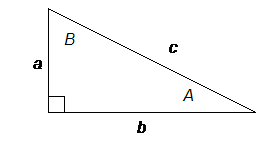
The usual labeling convention for right triangles is that the angles are capital letter A and B, and the sides are lower case letters a and b such that side a is opposite angle A, and side b is opposite angle B. The letter c is for the hypotenuse, which is always opposite the 90° angle. To talk about the trigonometric functions of an angle, it is more convenient to label the sides according to where they are in relation to the angle. Regardless of whether we are talking about angle A or angle B, one leg of the triangle will be opposite the angle in question, and one leg will be adjacent to it. Therefore, we will label the sides opposite and adjacent, depending on the location of the angle that we are talking about. The hypotenuse is a special case, and will just be called the hypotenuse. If we were interested in angle A, the diagram would look like this:

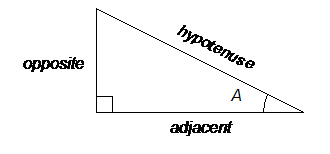
On the other hand, if angle B were the angle of interest, the diagram would look like this:

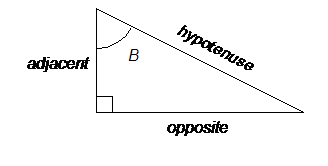
Now that we’ve gotten past the labeling, we need to make a couple of important observations:

1.     We only need to specify one angle to specify a family of similar right triangles.

Because it is given that we are only talking about right triangles, specifying a value for angle A will automatically force B to have a value of 90° − A. Since all three angles are known, the shape is determined. The only variable is the overall size of the triangle, which does not matter because…

2.     The ratios of sides are the same for all similar triangles.

For example, the following two triangles both have the same measure for angle A:

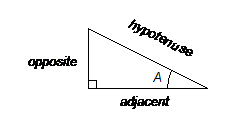
Although their sides are of different lengths, the ratio of pairs of sides is still the same. For example, if angle A measures 30°, we would find that the hypotenuse is always twice as long as the opposite side, no matter which triangle we use to make the measurements.

Taking the ratio of opposite over hypotenuse, we see that for an angle of 30°,

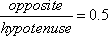
This ratio, then, is a function of only the measure of angle A. We call this function the sine of angle A, and denote it by

sin
30° = 0.5

There are six ratios that we can make out of the three sides of the triangle, and these ratios are the six trigonometric functions.

Of these six functions, only the three in the left column (sin, cos, and tan) are commonly used. This is because the others are just reciprocals of these three:

,  ,
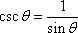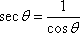and

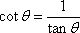
This is also why your calculator does not have buttons for csc, sec, and cot. For instance, if you wanted to know the cosecant of 25°, you would find the sine of 25° and then take its reciprocal.

CALCULATOR NOTE:
When your calculator computes a trigonometric function, it needs to know if the given angle is measured in degrees or radians. Obviously, the sine of an angle that measures 30 degrees is quite different from the sine of an angle that measures 30 radians. Your calculator will have a button on it that switches the mode from degrees to radians (and usually also grads, another system of angular measure that we will not use). Most calculators are in degrees mode by default, and when you switch to radians a small “rad” appears somewhere on the display. You must develop the habit of always verifying that your calculator is in the correct mode before you press any of the trig function buttons.