Trigonometric Functions of any Angle

Trigonometric Functions of any Angle

The problem with the right-triangle definition of the trig functions is that a right triangle can only contain angles between 0° and 90°, yet the trig functions are defined for all values, from negative infinity to positive infinity (except for certain points where some functions, such as the tangent, are undefined). To generalize the trig functions, we must abandon the right-triangle definition. In its place, we define them on a circle. To simplify things, we use a circle with a radius of one unit, called a unit circle. This circle is placed onstandard x–y coordinate axes:

Now we can draw a radius at any desired angle. The x-coordinate of the endpoint of this radius will be the cosine of the angle, and the y-coordinate will be the sine of the angle, provided that the angle is measured in standard position: counter-clockwise from the positive x-axis.If we draw the radius in the first quadrant, where 0° < θ < 90°, we will find that this new definition agrees with the old right-triangle definition. For example,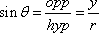, but since we said that   r = 1, we get sin θ = y.

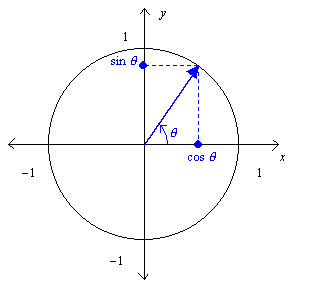
Now that the sine and cosine are defined, the tangent can be defined from them:

 ,
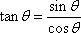because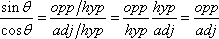 

This means the tangent will be undefined for any angle having a cosine equal to zero. This occurs at 90°, 270°, and plus or minus any multiple of 180° from these angles. Try it on your calculator and you will see that you get an error for the tangent of these values.

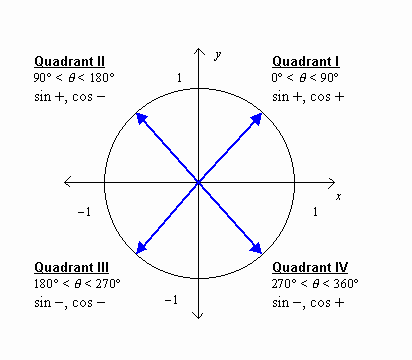
If the angle is not in the first quadrant, then the sine or the cosine (or both) will be negative, because the x– or y-coordinates will be negative. The following diagram shows the signs in each quadrant.

Other Angles

If an angle is greater than 360°, you can subtract multiples of 360° until it is between 0° and 360°. For example, sin 415° = sin 55° because 415 –