Solving Right Triangles

Solving Right Triangles

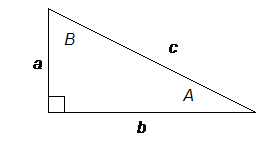
Solving a triangle means finding the values of all three sides and all three angles. In order to do this you need three pieces of information, one of which must be the length of a side. In the case of a right triangle, you already know that one angle is 90°, so you only need to know two additional things, one of which must be the length of a side. The tools you use to find the missing pieces are:

The Pythagorean Theorem

a² + b² = c²

If you know any two sides of a right triangle, you can use the Pythagorean theorem to solve for the unknown side.

The Sum of the Angles in any Triangle is 180° (or π radians)

A + B = 90°

Because a right triangle already has a 90° angle in it, the other two must add up to 90° (or π/2 radians). If you know one of the angles, then the other is found by subtracting from 90°

The Trigonometric Functions

Because trig functions are ratios of sides, if you know one angle and one side, you can find any otherside by using the appropriate trig function.

The Inverse Trigonometric Functions

If you know two sides but not anangle, you can find the value of a trig function by taking the ratio of the known sides, and then the inverse trig function will give you the correspondingangle.

NOTES

1.     Itis best to use the given values for each calculation, rather than usingcalculated values for subsequent calculations. If you make a mistake in a calculation, the error will be propagated through further calculations that use the incorrect value. In addition, a calculated value is usually rounded off,and this will affect the precision of further calculations.

2.     You will find that you don’t need to use all of the above tools to solve a given triangle. That means that you can use the unused tool as a check on your calculations. For example, if you did not use the Pythagorean theorem, then you could use it to verify that your results satisfy the Pythagorean theorem (to within your round-off precision).

Examples

Example 1: Given one side and one angle

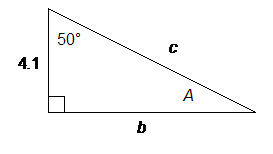
First, we can easily find the missing angle:

A = 90° − 50° = 40°

To find the missing sides, we usetrig functions.

Finding b

Notice that the known side (4.1) is adjacent to the known angle (50°). The unknown side b is opposite the given angle. The trig function that involves opposite and adjacent is the tangent, so we write

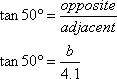
Now we just solve this for b:

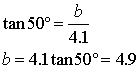
(rounded to one decimal place)

Finding c

Again notice that the known side is adjacent to the known angle (50°). The unknown side c is the hypotenuse. The trig function that involves hypotenuse and adjacentis the cosine, so we write

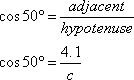
Now we solve for c:

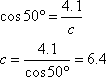
(rounded to one decimal place)

·       As a check, we can verify that the three sides satisfy the Pythagorean theorem:

4.1² + 4.9² = 6.4²

40.82 = 40.96  (we don’t expect this to be exact because we rounded off the numbers. However, it agrees to two significant figures, which is what we were using)

Example 2: Given two sides

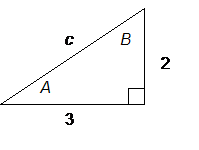
We can easily find the missing side from the Pythagorean theorem:

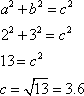
To find the missing angles we use inverse trig functions.

Finding A

Relative to angle A, the two given sides are the opposite and the adjacent, so we will use the tangent function.

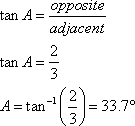
(rounded to one decimal place)

Finding B

Now that we know A, we can easily find B by subtracting A from 90°, but if we want to compute B using only the given values, we must proceed as before. Relative to angle B, the two given sides are the opposite and the adjacent (although in opposite roles from when we were considering angle A), so again we will use the tangent function.

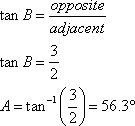
(rounded to one decimal place)

·     As a check, we can verify that A + B = 90°

Application

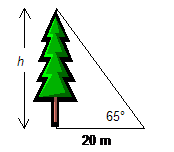
The angle of elevation to the top of a tree is 65° at a distance of 20 meters from the base of the tree. How tall is the tree?