Inverse Trig Functions
Given an angle, say 25°, you would calculate its sine by entering the number 25 in your calculator and then, after making sure that your calculator is in degrees mode, press the “sin” button to get 0.422618261741.
sin 25° = 0.422618261741
But what if you knew that an angle has a sine of 0.422618261741 but you don’t know what the angle is? You need to run the sine function backwards, reversing the roles of its input and output so that given 0.422618261741 it will output the value 25°. This is what the inverse sine function does. It is denoted by either
sin-1 0.422618261741 = 25°
or
arcsin 0.422618261741 = 25°
IMPORTANT: The use of a minus one superscript is bad notation (but we are stuck with it), because in this context it does NOT mean a negative one power. Raising something to the negative one power ordinarily means the same thing as taking its reciprocal:
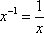
BUT THIS IS NOT WHAT IS HAPPENING HERE!
In the context of sin-1, the negative one exponent is in fact not an exponent at all. It is just a way of indicating the inverse function, which has nothing to do with the reciprocal. The inverse function is the function “run backwards.” This confusing notation will make you want to use the 1/x key on your calculator, but that would be wrong. To access the inverse trig functions on most calculators, you press the “2nd” key and then press the trig key, something like this:
0.422618261741 
 ,
,
Which should give a result of 25°.
There is a problem that arises in defining inverse trig functions, namely that more than one angle has a given sine (or cosine or tangent). In order to be a function, we must get one unique output for any given input. Theproblem becomes evident if we look at an example. The sine of 30° is 0.5, but the sine of 150° is also 0.5 (try it on your calculator).
sin 30° = 0.5
sin 150° = 0.5
Now suppose we want to know the inverse sine of 0.5. We would be asking the question “What angle has a sine of 0.5?”, but this question has at least two answers: 30° and 150°. If fact you can add or subtract multiples of 360° to these two answers to generate an infinite list of angles that have a sine of 0.5. However, if you try the inverse sine of 0.5 on your calclator, it will give you an answer of 30°.
sin-1
0.5 = 30°
Why did it give just that answer, and not the 150° answer? It is because the range of the inverse trig functions has been artificially restricted in order to make them behave like functions. Someone just decided that the inverse sine of 0.5 would be 30°, not 150°. It is important for you to remember that when your calculator gives you an angle from an inverse trig function, it is only one possible answer–there will always be other angles that have the same sine, cosine, or tangent.
