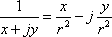AC Applications

Series LRC Circuit

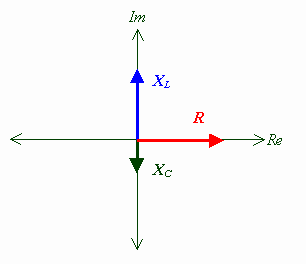
The usefulness of complex numbers in AC electronics comes from the fact that complex numbers automatically preserve the phase relationships caused by inductive and capacitive reactance. In a series RLC circuit, the voltage on the resistor is always in phase with the current, but the voltage drop across the inductor will by 90° ahead of the
current, and the voltage drop across the capacitor will be 90° behind the current. This means that the voltage on the inductor and capacitor are 180° out of phase with each other. Because of this, the total impedance of the circuit depends on the difference between the inductive reactance XL and the capacitive reactance XC.

This can be represented on a diagram, sometimes called an impedance phasor diagram:

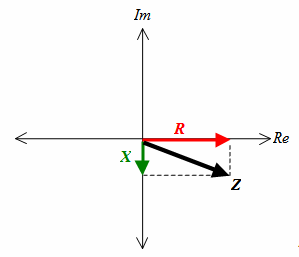
The pure resistance R  is always measured
along the positive real axis, the inductive reactance XL is along the positive imaginary axis, and the capacitive reactance XC is along the negative imaginary axis. The total impedance Z is the vector sum of these three vectors.

The real part of the impedance Z is the pure resistance R, while the imaginary part is the
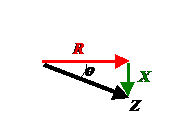
frequency-dependent reactance (XL− XC).

If we have only capacitance (or only inductance) then the diagram becomes a simple right triangle:

or

So by basic trigonometry, 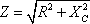 and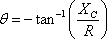 

In polar form, the net impedance is Z = Z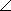θ.

In rectangular form it is simply Z = R − jXC

When both capacitance and inductance are present, the capacative and inductive impedences point in opposite directions and tend to cancel each other. Adding them together gives a net reactance along the imaginary axis:

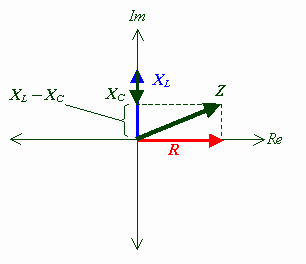       In rectangular form, Z = R + j (XL− XC)

The polar form is found from
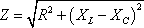and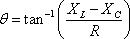

Parallel Resistance and Reactance

Since reactance is kind of like resistance, it is reasonable that when they are in parallel they will add as reciprocal, along with the ordinary resistances. The only thing that is different now is that you are adding complex numbers, so let’s look at the reciprocal of a complex number.

A reciprocal can be thought of as division (1 ÷ a number), it is best done in polar form. The number 1 written as a polar complex number is 1 0°, so the reciprocal of rθ is:

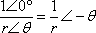
Just for the sake of completeness, the reciprocal in rectangular form looks like:

 

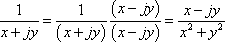
You might notice that the denominator ends up being just r2, where 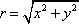 ,    so