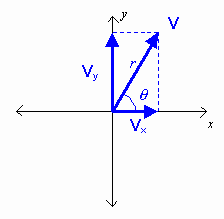
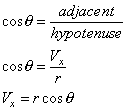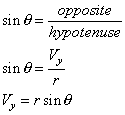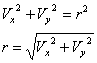Best Algebra Homework Help Websites
When it concerns obtaining assist with Algebra homework, there are lots of sites to pick from. Just how do you recognize which one is the very best for you? And also a lot more notably, exactly how do you recognize that the web site you pick is reliable and will really help you learn and understand the material?
Here are some tips for discovering the best Algebra homework help websites:
– Look for a site that offers detailed descriptions of the concepts you’re battling with. This will certainly help you not just comprehend the material better, but also be able to resolve similar troubles by yourself in the future.
Where to Get Help with Algebra Homework?
Along with internet sites, there are additionally a variety of applications that can be made use of for help with Algebra research. These apps use a selection of attributes, including step-by-step options, technique issues, and graphing devices.
– Check out testimonials of the web site prior to using it. See what various other students have actually said concerning their experience utilizing it. This can give you some insight into whether the website is in fact useful and easy to use.
Where to Get Help with Algebra Homework?
There are a variety of websites that pupils can utilize for aid with Algebra homework. Several of the most prominent sites consist of Khan Academy, Mathway, and also WebMath. These web sites offer a range of sources, consisting of tutorials, step-by-step solutions, and also method troubles.
– Make sure the internet site has a variety of resources, such as video lessons, technique quizzes, and also printable worksheets. This will allow you to discover the format that works finest for you as well as makes certain that you have every little thing you need in one area.
Finally, pupils can additionally obtain aid with Algebra homework by talking with their instructor or choosing a tutor. Teachers and tutors can use individually aid and also support on specific subjects or problem areas. They can additionally offer helpful resources, such as worksheets and technique problems.
How to Choose the Best Algebra Assignment Help Website?
If you’re looking for help with your algebra homework, you may be wondering how to choose the best web site for obtaining that assistance. Below are a couple of pointers to help you discover the most effective algebra homework help site:
- Make sure the site is trusted and has actually been around for a while.
- Ensure the site has a good online reputation and also is very ranked by past consumers.
- Check out the site’s FAQs and also other details web pages to ensure they offer what you require.
- Make sure the site has an excellent customer support division in case you have any type of questions or troubles.
- Compare costs in between different sites to make sure you’re getting the best deal.
Top Algebra Homework Help Websites
When it pertains to algebra homework aid, the web is a found diamond of resources. From video tutorials to skilled guidance, there’s no shortage of web sites that can use support. Yet with numerous choices available, it can be tough to recognize where to start. That’s why we’ve assembled this list of the top algebra homework help websites.
AssignCode.com Review
If you are seeking the most effective algebra homework help website, look no more than AssignCode.com. Our experts are available 24/7 to aid you with any kind of and all of your algebra needs. We will not just solve your issues, yet also educate you just how to resolve them yourself so that you can be successful in the future.
AssignCode.com is the most effective web site for obtaining assist with your algebra homework. Our experts are offered 24/7 to address your troubles and show you exactly how to solve them yourself so that you can be successful in the future. Furthermore, our service is budget-friendly and also easy to use. We offer a straightforward system that makes getting help with your algebra homework a wind. So if you are trying to find the very best area to get aid with your algebra research, look no further than AssignCode.com!
AssignMaths.com Review
If you’re trying to find a trusted site to help with your algebra homework, look no more than AssignMaths.com. This online source is among one of the most trusted and also well-established in the field, using professional help with every little thing from fundamental equations to complicated problems. Most importantly, the solution is entirely complimentary – there’s no need to subscribe or register. Just get in the problem you’re dealing with and get an immediate service from one of AssignAlgebras’ knowledgeable tutors.
The professionals at AssignCode.com are readily available 24/7 to help you with any type of and all of your algebra needs. They will not just resolve your problems, yet likewise educate you exactly how to address them yourself to make sure that you can be successful in the future. Furthermore, our service is economical and also easy to use. We supply an easy to use system that makes getting aid with your algebra research a wind. So if you are searching for the very best algebra homework help website, look no more than AssignCode.com!
- Professional aid – AssignMaths.com supplies experienced assist with algebra homework, from standard formulas to complicated problems.
- Free solution – There’s no need to sign up or sign up to use this online resource. It’s completely totally free!
- Instantaneous service – Get an instantaneous option to your algebra homework troubles from among AssignAlgebras’ skilled tutors.
- Convenient – Get assist with your algebra homework anytime and also anywhere you require it, with AssignMaths.com’s on-line service.
Cwassignments.com Review
CWAssignments.com’s online research service offers a number of benefits over various other solutions:
- Professional help – obtain professional help with your algebra research from one of our seasoned tutors.
- Free solution – there is no requirement to register or register to use our solution, which is completely free.
- Instantaneous option – obtain an instant option to your algebra homework problems from among our seasoned tutors.
- Convenient – get help with your algebra research anytime and anywhere you need it, with CWAssignments.com’s on-line solution.
CWAssignments.com is a reliable online resource that provides specialist assist with algebra homework from seasoned tutors. The solution is cost-free, and you can obtain assist anytime and also anywhere you require it.
CodingPedia.org Review
If you’re searching for a detailed online source to assist you with your algebra research, look no further than CodingPedia.org. This site provides a variety of tutorials and explanations on every little thing from basic procedures to solving formulas, making it the excellent one-stop shop for all your algebra needs. Most importantly, the site is completely free to utilize, so there’s no factor not to give it a try!
If you’re searching for a detailed online resource to help you with your algebra research, look no further than CodingPedia.org. This web site uses a large range of tutorials and also explanations on everything from standard procedures to fixing equations, making it the perfect one-stop purchase all your algebra requires. Best of all, the site is totally cost-free to make use of, so there’s no reason not to give it a try! Some of the advantages of using CodingPedia.org for homework assistance consist of:
- The website has a big amount of info on algebra subjects, so you can be certain to locate whatever you need.
- All the content is easy to understand as well as well-organized, so you can rapidly find what you’re searching for.
- The site is updated routinely, so you can be certain that the information is current.
- There are lots of interactive exercises to assist you practice your skills, so you can enhance your understanding.
- The community forum is a fantastic place to obtain help from various other pupils if you obtain stuck on an issue.
CodingPedia.org is an impressive online source for anyone seeking aid with algebra research. The site provides a wide range of tutorials and also explanations on every little thing from basic operations to resolving formulas, making it the best one-stop purchase all your algebra needs. Most importantly, the site is entirely cost-free to make use of, so there’s no reason not to give it a try! A few of the advantages of using CodingPedia.org for research help consist of:
1) The site has a substantial amount of information on algebra topics, so you can be sure to find whatever you need;
2) All the material is understandable and also efficient, so you can quickly locate what you’re trying to find;
3) The website is upgraded routinely, so you can be certain that the details is updated;
4) There are a lot of interactive exercises to aid you practice your abilities, so you can improve your understanding;
5) The neighborhood discussion forum is a terrific location to get assist from other students if you obtain stuck on an issue.
If you’re struggling with algebra homework, do not be reluctant to visit CodingPedia.org– it’s most definitely worth a try!
DoMyAssignments.com Review
DoMyAssignments.com is just one of the best Algebra homework help websites readily available online. It provides students with a wide variety of services that can help them get through their Algebra training course with flying colors. The internet site has a group of specialists who are greater than capable of assisting pupils with their Algebra research, and it additionally has a money-back warranty if pupils are not pleased with the outcomes.
The benefits of using DoMyAssignments.com for research assistance include:
- Specialist aid with Algebra homework from a team of professionals.
- Surefire contentment or a money-back refund.
- 24/7 on the internet support for trainees.
- A variety of services that can help trainees get through their Algebra course with flying shades.
DoMyAssignments.com is a great website that supplies students with specialist aid for their Algebra research. The team of professionals on the web site are greater than capable of helping trainees make it through their Algebra training course, and the money-back guarantee ensures contentment. The large range of services readily available on DoMyAssignments.com can also help trainees get through their program with flying shades.