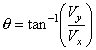|
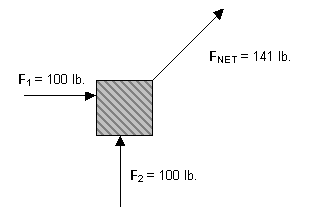
Now we come to the question of how vectors add. Recall the example from the previous page: In this example, two 100-lb. forces add up to a 141-lb. force in a different direction. To see how this comes about, notice that we can take the three arrows from the picture and make a triangle out of them: This shows how to add vectors geometrically:
In this example the two vectors were perpendicular, so we got a right triangle. This lets us use the Pythagorean theorem to find the length of the resultant vector, which is the hypotenuse of the triangle. Because both vectors were the same length, the angle will be 45°. If the two vectors were different lengths, you could use the inverse tangent function to find the angle. Adding Vectors that are Not Perpendicular Adding Vectors Geometrically If the two vectors were not perpendicular, we would not have a right triangle, and we could not use the Pythagorean theorem or the basic trig functions to find the length and angle of the resultant. There are ways to solve these triangles with trigonometry, called the law of cosines and the law of sines, but we are not going to learn about Adding by Components There is another method, which uses the rectangular components of the vectors. This method always works, but it can be a bit tedious and requires careful bookkeeping.
|