Substitution Method
When we used the Addition Method to solve a system of equations, we still had to do a substitution to solve for the remaining variable. With the substitution method, we solve one of the equations for one variable in terms of the other, and then substitute that into the other equation. This makes more sense with an example:
Example:
| 2y + x = 3 | (1) |
| 4y – 3x = 1 | (2) |
Equation 1 looks like it would be easy to solve for x, so we take it and isolate x:
| 2y + x = 3 | |
| x = 3 – 2y | (3) |
Now we can use this result and substitute 3 – 2y in for x in equation 2:
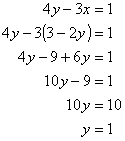
Now that we have y, we still need to substitute back in to get x. We could substitute back into any of the previous equations, but notice that equation 3 is already conveniently solved for x:
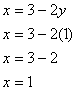
And so the solution is (1, 1).
As a rule, the substitution method is easier and quicker than the addition method when one of the equations is very simple and can readily be solved for one of the variables.
