Addition Method
The whole problem with solving a system of equations is that you cannot solve an equation that has two unknowns in it. You need an equation with only one variable so that you can isolate the variable on one side of the equation. Both methods that we will look at are techniques for eliminating one of the variables to give you an equation in just one unknown, which you can then solve by the usual methods.
The first method of solving systems of linear equations is the addition method, in which the two equations are added together to eliminate one of the variables.
Adding the equations means that we add the left sides of the two equations together, and we add the right sides together. This is legal because of the Addition Principle, which says that we can add the same amount to both sides of
an equation. Since the left and right sides of any equation are equal to each other, we are indeed adding the same amount to both sides of an equation.
Consider this simple example:
Example:
![]()
If we add these equations together, the terms containing y will add up to zero (2y plus –2y), and we will get
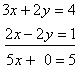
or
5x = 5
x = 1
However, we are not finished yet—we know x, but we still don’t know y. We can solve for y by substituting the now known value for x into either of our original equations. This will produce an equation that can be solved for y:
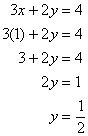
Now that we know both x and y, we can say that the solution to the system is the pair (1, 1/2).
This last example was easy to see because of the fortunate presence of both a positive and a negative 2y. One is not always this lucky. Consider
Example:
![]()
Now there is nothing so obvious, but there is still something we can do. If we multiply the first equation by –3, we get
![]()
(Don’t forget to multiply every term in the equation, on both sides of the equal sign). Now if we add them together the terms containing x will cancel:
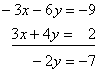
or
![]()
As in the previous example, now that we know y we can solve for x by substituting into either original equation. The first equation looks like the easiest to solve for x, so we will use it:
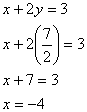
And so the solution point is (–4, 7/2).
Now we look at an even less obvious example:
Example:
![]()
Here there is nothing particularly attractive about going after either the x or the y. In either case, both equations will have to be multiplied by some factor to arrive at a common coefficient. This is very much like the situation you face trying to find a least common denominator for adding fractions, except that here we call it a Least Common Multiple (LCM). As a general rule, it is easiest to eliminate the variable with the smallest LCM. In this case that would be the y, because the LCM of 2 and 3 is 6. If we wanted to eliminate the x we would have to use a LCM of 10 (5 times 2). So, we choose to make the coefficients of y into plus and minus 6. To do this, the first equation must be multiplied by 3, and the second equation by 2:
![]()
or
Now adding these two together will eliminate the terms containing y:
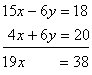
or
x = 2
We still need to substitute this value into one of the original equations to solve for y:
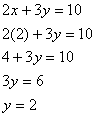
Thus the solution is the point (2, 2).
