Roots
Definition
Roots are the inverse of exponents. An nth root “undoes” raising a number to the nth power, and vice-versa. (The correct terminology for these types of relationships is inverse functions, but powers and roots can only be strictly classified as inverse functions if we take care of some ambiguities associated with plus or minus signs, so we will not worry about this yet). The common example is the square root, which “undoes” the act of squaring. For example, take 3 and square it to get 9. Now take the square root of 9 and get 3 again. It is also possible to have roots related to powers other than the square. The cube root, for example, is the inverse of raising to the power of 3. The cube root of 8 is 2 because 23 = 8. In general, he nth root of a number is written:
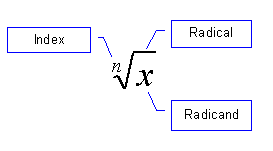
![]() if and only if
if and only if ![]()
![]() because 43 = 64
because 43 = 64
We leave the index off the square root symbol only because it is the most common one. It is understood that if no index is shown, then the index is 2.
![]() if and only if
if and only if ![]()
![]() because 42 = 16
because 42 = 16
Square Roots
The square root is the inverse function of squaring (strictly speaking only for positive numbers, because sign
information can be lost)
Principal Root
- Every positive number has two square roots, one positive and one negative
Example: 2 is a square root of 4 because 2 ´ 2 = 4, but –2 is also a square root of 4 because (–2) ´ (–2) = 4
To avoid confusion between the two we definethe symbol ![]() (this symbol is called a radical) to mean the principal or positive square root.
(this symbol is called a radical) to mean the principal or positive square root.
The convention is:
For any positive number x, ![]() is the positive root,and
is the positive root,and ![]() is the negative root.
is the negative root.
If you mean the negative root, use a minus sign in front of the radical.
Example:
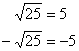
Properties
![]() for all non-negative numbers x
for all non-negative numbers x
![]() for all non-negative numbers x
for all non-negative numbers x
However, if x happens to be negative, then squaring it will produce a positive number, which will have apositive square root, so
![]() for all real numbers x
for all real numbers x
· You don’t need the absolute value sign if you alreadyknow that x is positive. For example, ![]() , and saying anything about the absolute value of 2 would be superfluous. You only need the absolute value signs when you are taking the square root of a square of a variable, which may be positive or negative.
, and saying anything about the absolute value of 2 would be superfluous. You only need the absolute value signs when you are taking the square root of a square of a variable, which may be positive or negative.
· The square root of a negative number is undefined, because anything times itself will give a positive (or zero) result.
![]() (your calculator will probably say ERROR)
(your calculator will probably say ERROR)
· Note: Zero has only one square root (itself). Zero is considered neither positive nor negative.
WARNING: Do not attempt to do something like the distributive law with radicals:
![]() (WRONG) or
(WRONG) or ![]() (WRONG). This is a violation of the order of operations. The radical operates on the result of everything inside of it, not individual terms. Try it with numbers to see:
(WRONG). This is a violation of the order of operations. The radical operates on the result of everything inside of it, not individual terms. Try it with numbers to see:
![]() (CORRECT)
(CORRECT)
But if we (incorrectly) do the square roots first, we get
![]() (WRONG)
(WRONG)
However, radicals do distribute over products:
![]()
and
![]()
provided that both a and b are non-negative (otherwise you would have the square root of a negative number).
Perfect Squares
Some numbers are perfect squares, that is, their square roots are integers:
0, 1, 4, 9, 16, 25, 36, etc.
It turns out that all other whole numbers have irrational square roots:
![]() ,
, ![]() ,
, ![]() ,
, ![]() etc. are allirrational numbers.
etc. are allirrational numbers.
· The square root of an integer is either perfect or
irrational
