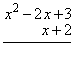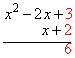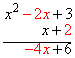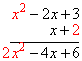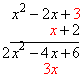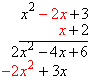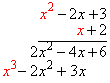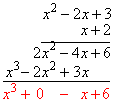Multiplication of Polynomials
- The general rule is that each term in the first factor has to multiply each term in the other factor
- The number of products you get has to be the number of terms in the first factor times the number of terms in the second factor. For example, a binomial times a binomial gives four products, while a binomial times a trinomial gives six products.
- Be very careful and methodical to avoid missing any terms
- After the multiplication is complete you can try to collect like terms to simplify the result
Example: Product of a binomial and a trinomial
(x + 2)(x2– 2x + 3)
There are six possible products. We can start with the x and multiply it by all three terms in the other factor, and then do the same with the 2. It would look like this:
(x+ 2)(x2– 2x + 3)
=(x)x2–(x)2x + (x)3 + (2)x2–(2)2x + (2)3
= x3– 2x2 + 3x + 2x2– 4x + 6
= x3– x + 6
This method can get hard to keep track of when there are many terms. There is, however, a more systematic method based on the stacked method of multiplying numbers:
|
Stack the factors, keeping like degree terms lined up vertically: |
|
|
Multiply the 2 and the 3: |
|
|
Multiply the 2 and the –2x: |
|
|
Multiply the 2 and the x2: |
|
|
Now multiply the x by each term above it, and write the results down underneath, keeping like degree terms lined up vertically: |
|
|
|
|
|
|
|
|
Then you just add up the like terms that are conveniently stacked above one another: |
|
This stacked method is much safer, because you are far less likely to accidentally overlook one of the products, but it does take up more space on the paper.
Product of a monomial and a binomial: Distributive Law
Example: ab(2a + 1) = ab(2a) + ab(1) = 2a2b + ab
Product of two binomials: FOIL (First-Outer-Inner-Last)
Because the situation of a binomial times a binomial is so common, it helps to use a quick mnemonic device to help remember all the products. This is called the FOIL method.
Example:
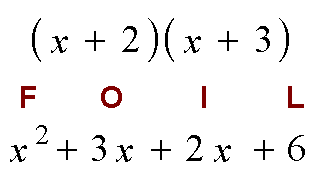
1. The F stands for first, which means the x in the first factor times the x in the second factor
2. The O stands for outer, which means the x in the first factor times the 3 in the second factor
3. The I stands for inner, which means the 2 in the first factor times the x in the second factor
4. The L stands for last, which means the 2 in the first factor times the 3 in the second factor
· Of course you would then combine the 3x + 2x into a 5x, because they are like terms, so the final result is